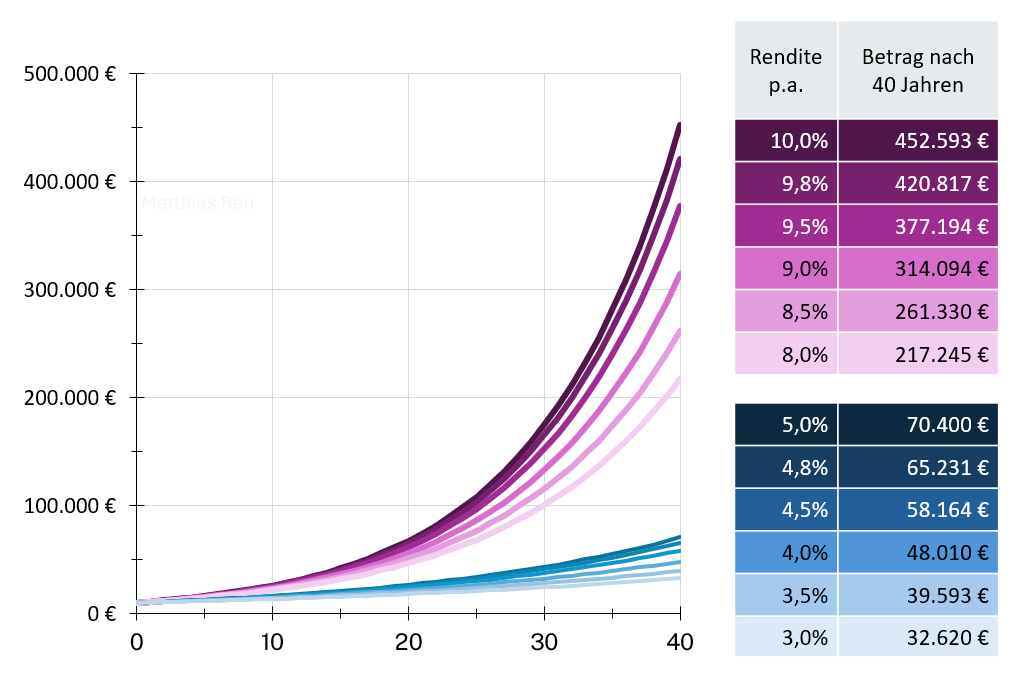
Die Sache mit dem exponentiellen Wachstum ist alles andere als intuitiv und nicht wirklich fassbar: Eine Einmalanlage von 10.000 € wächst bei einer jährlichen Rendite von 5 % in 40 Jahren auf 70.400 €. Die doppelte Rendite ergibt 452.593 € und damit 6,5-Mal mehr. Bei der jährlichen Rendite von 10 % wächst das Vermögen im letzten Jahr um 41.145 €. Dieser Zuwachs ist viermal größer als die Anfangsinvestition. Hinten ist die Ente fett!
Warren Buffett ist auch reich, weil er alt ist
So hat auch Investmentlegende Warren Buffett erst nach seinem 65sten Geburtstag den größten Teil seines Vermögens „verdient“. Je nach Artikel sind es 85 % bis 99 %, was bezogen auf die absoluten Zahlen hohe Spannen bedeutet. Das Veröffentlichungsdatum der Artikel muss dabei berücksichtigt werden, denn je höher die Aktien seines Unternehmens Berkshire Hathaway stehen, desto höher ist sein Vermögen und desto höher ist auch der Anteil. Zudem muss berücksichtigt werden, dass er mittlerweile schon über 57 Milliarden US-Dollar gespendet hat. Sein aktuelles Vermögen beträgt ca. 160 US-Dollar. Im Jahr soll es zwischen 10 und 13 Milliarden US-Dollar betragen haben. In Bezug auf das aktuelle Vermögen und die Spenden müsste er demnach um die 95 % seines Vermögens nach seinem 65sten Geburtstag „verdient“ haben.
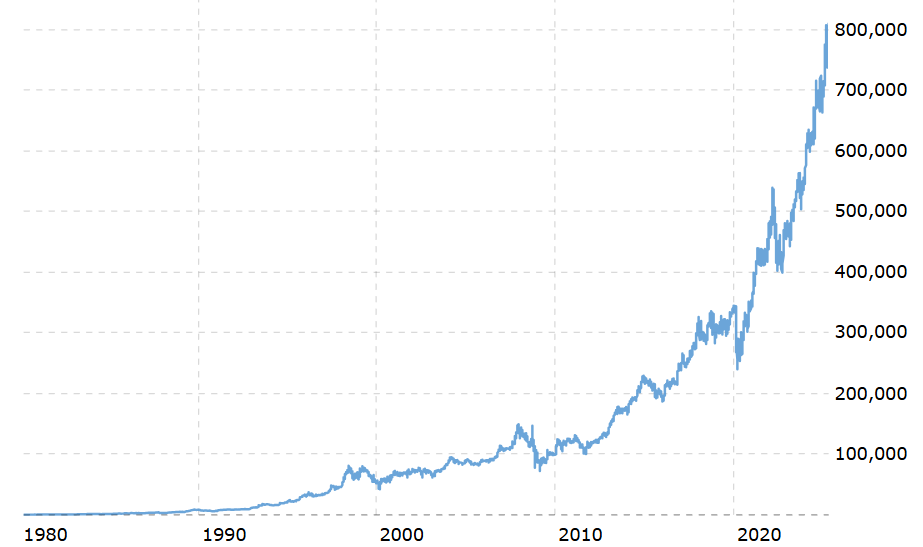
Warren Buffett ist also auch deswegen so reich, weil er früh mit seiner Geschäftstätigkeit und dem Investieren begonnen hat, damit nie aufhörte und sparsam lebte. Der Zinseszinseffekt konnte sich voll entfalten. Seine erste Aktie kaufte er 1942 im Alter von 11 Jahren. 2025 ist er 94 Jahre alt. Es gibt nicht viele Menschen auf der Welt, die seit 83 Jahren Geld investieren!
Der Zinseszinseffekt wird unterschätzt
„lol das kann jeder Schüler der 8. Klasse berechnen und musste es in der Schule auch tun.“
Diesen Kommentar rotzte mir jemand unter einen Beitrag zum Thema Zinseszinseffekt bzw. exponentielles Wachstum bei LinkedIn.
Inhaltlich stimme ich ihm zu und schreibe es immer wieder: Die Grundlagen für Finanzbildung werden in jeder Schule vermittelt. In Mathematik wird Prozentrechnung gelehrt und in Biologie wird exponentielles Wachstum im Rahmen der Bakterienvermehrung vermittelt. In vielen Bundesländern gibt es zudem die Fächer Wirtschaft, Politik, Gesellschafts- oder Gemeinschaftskunde, in denen die Themen Geld und Geldanlage zumindest oberflächlich unterrichtet werden; meistens leider zu theoretisch und langweilig.
Mir ging es darum, wie wenig intuitiv Exponentialfunktionen sind. Die Berechnung bekommen die meisten vielleicht noch hin. Bei einer Schätzung vermute ich, dass fast alle die Ergebnisse weit verfehlen, wenn sie dazu befragt würden.
Verlass dich nicht auf deine Intuition!
Dabei ist es beim Thema Geldanlage problematisch, dass man sich allzu oft auf seine Intuition und Schätzung verlässt, statt den Taschenrechner zu verwenden. Und so fallen Leute auf dubiose Angebote herein, in denen 2 bis 3 % Rendite pro Monat versprochen werden oder gar eine Verdopplung der Investition innerhalb von wenige Monaten.
Auch werden (direkte und indirekte) Kosten der Geldanlage oft unterschätzt. Kosten von 2 % pro Jahr klingen für Laien wenig. Bei einer Einmalanlage mit einer Anlagedauer von 40 Jahren führen sie dazu, dass das Endergebnis um knapp die Hälfte geringer ausfällt gegenüber einer kostengünstigen Alternative, egal ob die Rendite vor Kosten nun 5 % oder 10 % p. a. beträgt, wie die obige Grafik zeigt.
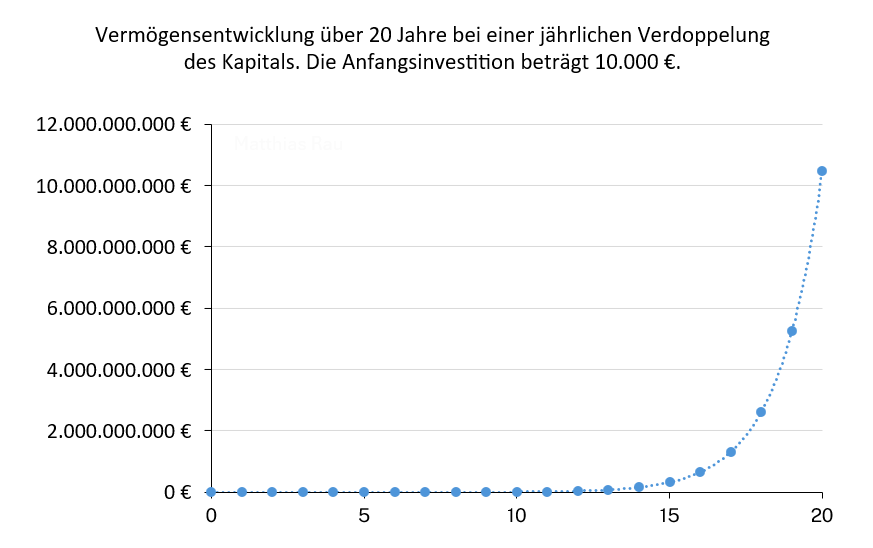
Der Zinseszinseffekt ist aberwitzig, insbesondere bei hohen Renditen oder langen Dauern. Eine jährliche Verdopplung von 10.000 Euro ergeben nach 20 Jahren über zehn Milliarden Euro! Wer also glaubt, dass dubiose Finanzanbieter 100 % Rendite pro Jahr erwirtschaften können, sollte den Taschenrechner heranziehen und hinterfragen, wie realistisch diese Versprechen denn sein können.
Eine logarithmische Skala wäre zur Darstellung exponentieller Funktionen angebrachter, aber auf den ersten Blick weniger beeindruckend.